논문 리뷰 💬 [Speculative Contrastive Decoding]
Paper
https://arxiv.org/pdf/2311.08981
Abstract
본 논문은 smaller LM을 활용해 speculative decoding과 contrastive decoding을 합친 speculative contrastive decoding (SCD)를 제시하여 추론 속도 향상 + 좋은 성능을 내는 디코딩 방법을 고안한다.
Introduction
LM은 추론 시 auto-regressive하게 토큰을 생성하기 때문에, 불가피하게 추론 시에는 많은 계산 비용을 사용한다. speculative decoding (SD)은 smaller LM이 다수의 연속적인 토큰을 생성한 뒤, 생성된 토큰을 larger model이 검토하며 쓸만한 토큰은 살리고 잘못된 토큰은 large model의 출력으로 대체한다. 만약 smaller LM이 쓸만한 토큰을 많이 생성하면, 추론 속도는 larger LM이 하나하나 auto-regressive하게 생성하는 것보다 훨씬 빨라질 수 있다.
추론 비용뿐 아니라 generation quality 역시 중요한 요소인데, contrastive decoding (CD)은 이를 가능케 하는 디코딩 방법이다. CD는 smaller LM이 아마추어적인 성향 (에러)를 훨씬 많이 발생시키기 때문에, large LM 확률 분포에서 small LM 확률 분포를 빼면 large LM의 전문가적 성향만 남기고 아마추어적 성향을 제거할 수 있다는 디코딩 방법이다.
SD와 CD는 모두 small LM을 이용해서 각각 auto-regressive generation의 inference acceleration과 quality improvement를 이뤘다.
Preliminaries
small LM을 Ma, large LM을 Me라고 하자.
Contrastive Decoding
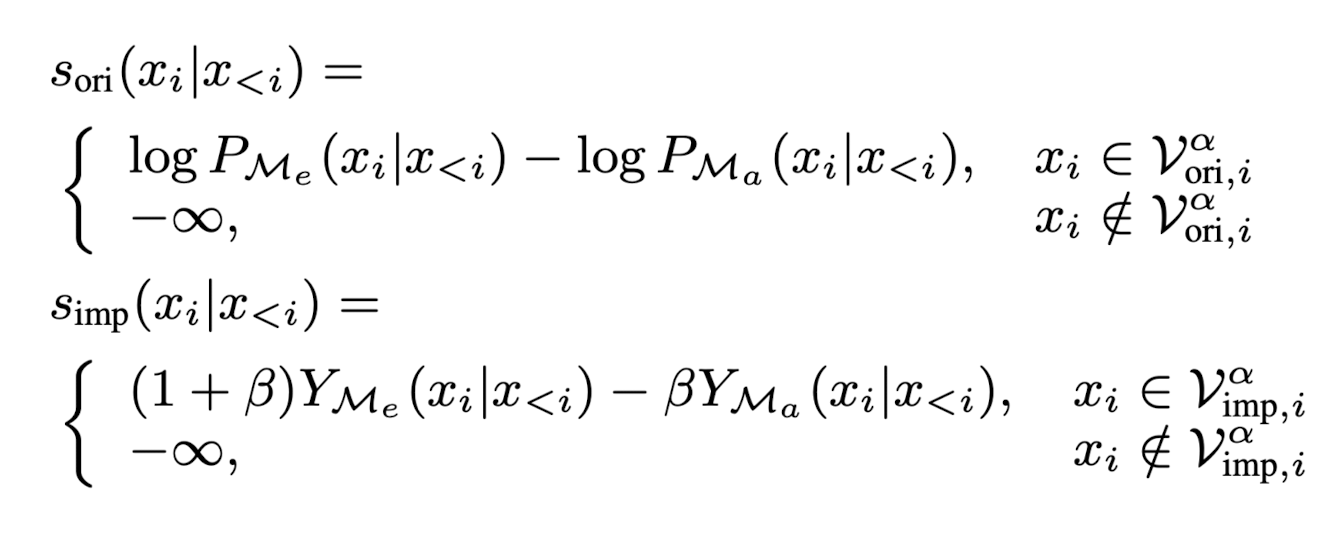
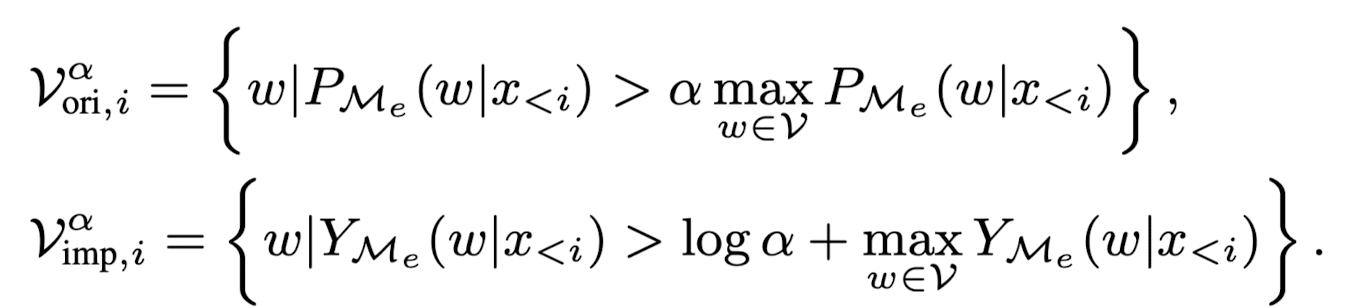

Speculative Decoding
- Ma가 한 번에 \(\gamma\)개의 연속적인 토큰을 생성한다.
- Me가 1에서 생성된 \(\gamma\)개의 토큰의 validity를 확인한다. (한 번 쭉 돈다)
- 만약 모든 \(\gamma\)개의 토큰이 accept되면, Me는 \(\gamma\)+1번째 토큰을 생성한다. 만약 Me가 \(\gamma\)개의 토큰 중에서 reject되는 것이 있으면 Me가 생성한 토큰으로 rejected token을 대체한다. 또한, 이 경우에는 추가적으로 토큰을 생성하지 않고 \(\gamma\)개의 토큰까지만 생성된 상태다.
만약 cost Me / cost Ma (cost efficient; c)가 충분히 낮고 Ma의 token acceptance가 높다면 Me는 한 번의 루프로 여러 개의 토큰을 생성할 수 있게 된다.
Speculative Contrastive Decoding
- Ma는 한 번에 \(\gamma\)개의 연속적인 토큰을 생성한다.
- Me가 토큰들의 유효성을 판단할 때 사용하는 target distribution을 Me의 원래 확률 분포가 아니라 contrastive decoding을 한 distribution Pn을 이용한다. Ma의 각 토큰은 \(\frac{P_n^{\tau}(x)}{P_{M_e}(x)}\)의 확률로 accept되고 1 - \(\frac{P_n^{\tau}(x)}{P_{M_e}(x)}\)의 확률로 reject된다. 아래 알고리즘의 6번째 줄의 \(r_i > \frac{P_n^{\tau}(x)}{P_{M_e}(x)}\)은 토큰이 reject되는 경우를 의미한다. 즉, 만약 \(\gamma\)개의 토큰 중 reject되는 토큰이 존재하면 (if) reject된 토큰을 Me의 확률 분포로부터 생성된 토큰으로 대체하고 거기까지만 최종 생성된 토큰으로 간주한 뒤 디코딩을 계속한다. 만약 Ma의 모든 토큰이 accept된 경우 (else) \(\gamma\)+1번째 토큰을 contrastive decoding을 이용해 만들어진 확률 분포로부터 생성하고 처음부터 \(\gamma\)+1번째까지 최종 생성된 토큰으로 간주한 뒤 디코딩을 계속한다.
SCD가 일반 SD와 다른 점은, 6번째 줄에서 SD가 Ma 토큰의 validity를 검사할 때 target distribution으로 Me가 아니라 Me-Ma의 contrastive distribution을 사용했다는 것과 13번째 줄에서 Ma의 모든 토큰이 accept되어 \(\gamma\)+1번째 토큰을 생성할 때 Me로부터가 아니라 Me-Ma의 contrastive decoding으로부터 생성했다는 것이다. 즉, SD에 CD를 적용했다는 것이다.

실험 결과를 간단히 살펴보면 SCD는 Ma, Me, SD보다 더 높은 성능을 내고 CD와는 비슷한 성능을 낸다.

또한, SCD는 SD를 이용하기 때문에 추론 속도가 가속화된다. (high expected acceleration factor)E.A factor는 아래와 같이 계산된다. \(\gamma\)는 한 번의 반복에서 Ma가 생성하는 토큰 수, \(\lambda\)는 Ma의 토큰이 Me에게 accept될 empirical acceptance rate, c는 Ma와 Me의 비용 계수다. 즉, E.A factor는 SD를 이용했을 때 몇 배나 추론 속도가 향상되는지를 의미한다.

결론적으로, SCD는 CD로 디코딩 성능도 높이면서 SD처럼 추론 속도도 빨리 할 수 있는 디코딩 방법이다.