1. Self-Attention
기존의 RNN 모델에는 크게 두 가지의 문제점이 있었다.
- linear interaction distance: 단어들 사이에 O(sequence length)의 선형 복잡도가 있음 -> long-distance dependency가 학습되지 않음.
- lack of parallelizability: RNN은 왼쪽에서 오른쪽으로 순차적으로 계산이 진행됨 -> 큰 데이터셋에 대해서는 학습이 느려짐.
그렇다면 attention은 어떻게 RNN의 문제점을 해결했을까? 전통적인 attention은 decoder의 hidden state를 query로 나타내고 encoder의 입력을 value와 key로 나타낸다. query와 key의 유사도(attention score)를 사용하여 value의 가중 평균을 구한 것이 attention output이다. self-attenttion은 전통적인 attention과는 다르게 input과 target의 관계보다는 input 단어 사이의 관계에 대해 학습한다. self-attention에서 각각의 단어는 query, key, value 세 가지 형태로 나타낸다. 예를 들어 한 단어의 query는 자신을 포함한 모든 단어의 key들과 부드럽게 연결되어 유사도(attention score)를 계산한다. 이 유사도가 key에 대응하는 value에 가중 평균이 되어 attention output이 만들어진다. self-attention은 한 단어와 다른 모든 단어 사이의 유사도를 검사하기 때문에 일단 linear interaction distance 문제가 해결된다. 또한 self-attention을 계산할 때 X, Q, K, V의 행렬 꼴로 만들어주면 병렬적으로 연산이 가능하기 때문에 lack of parallelizability 문제도 해결 가능하다.
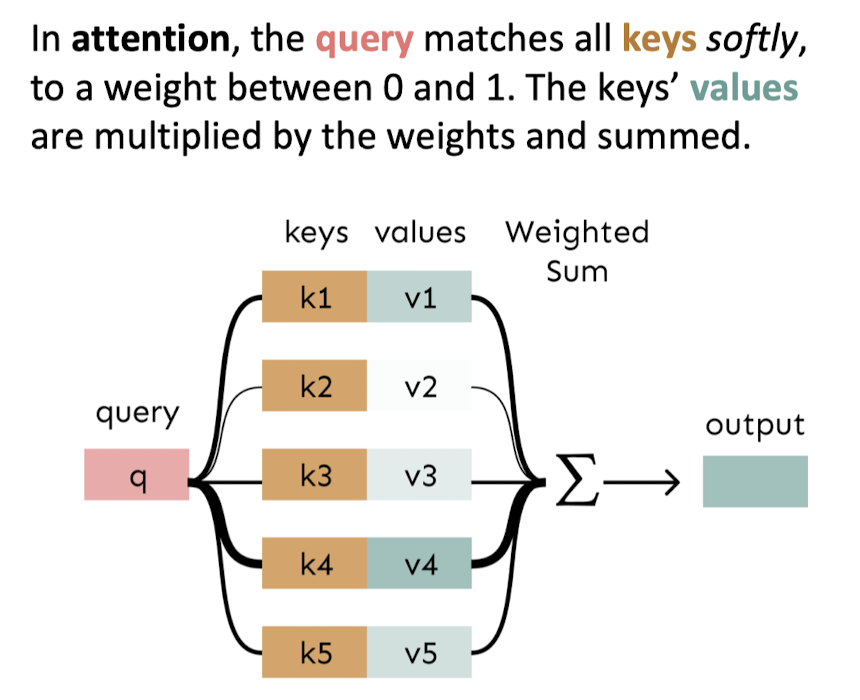
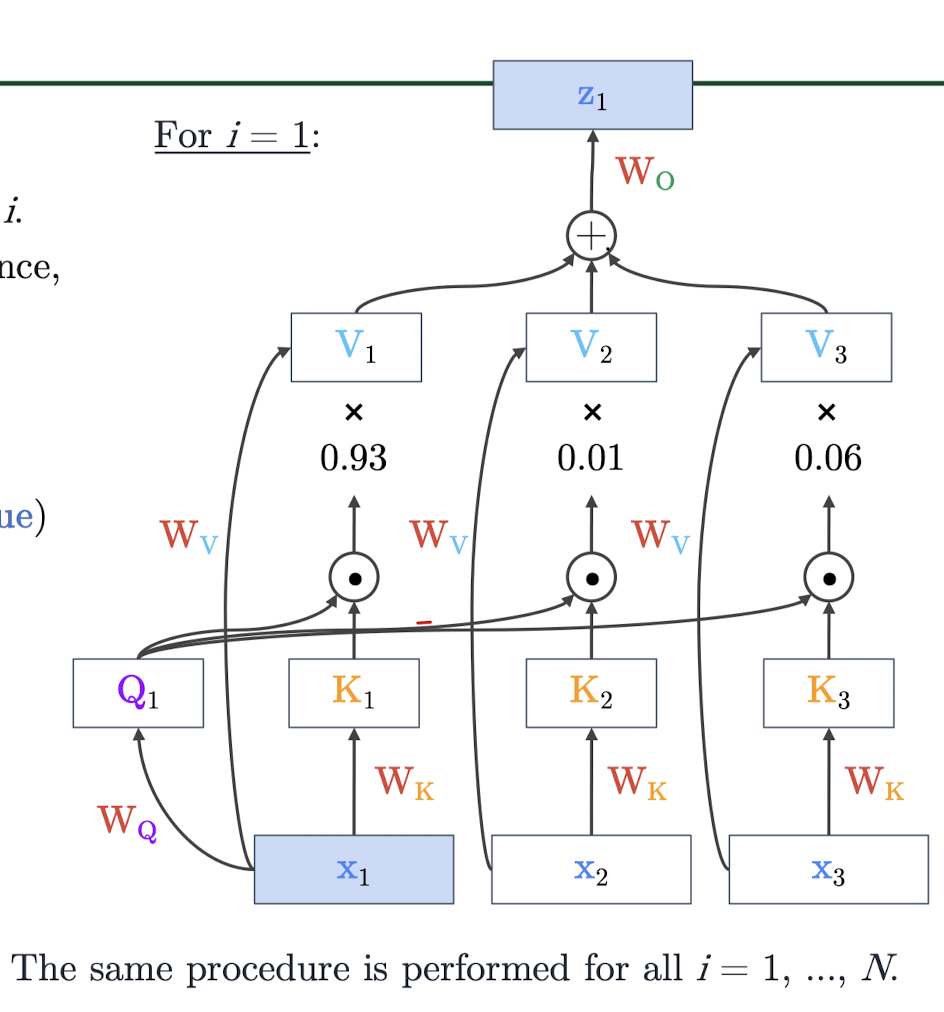
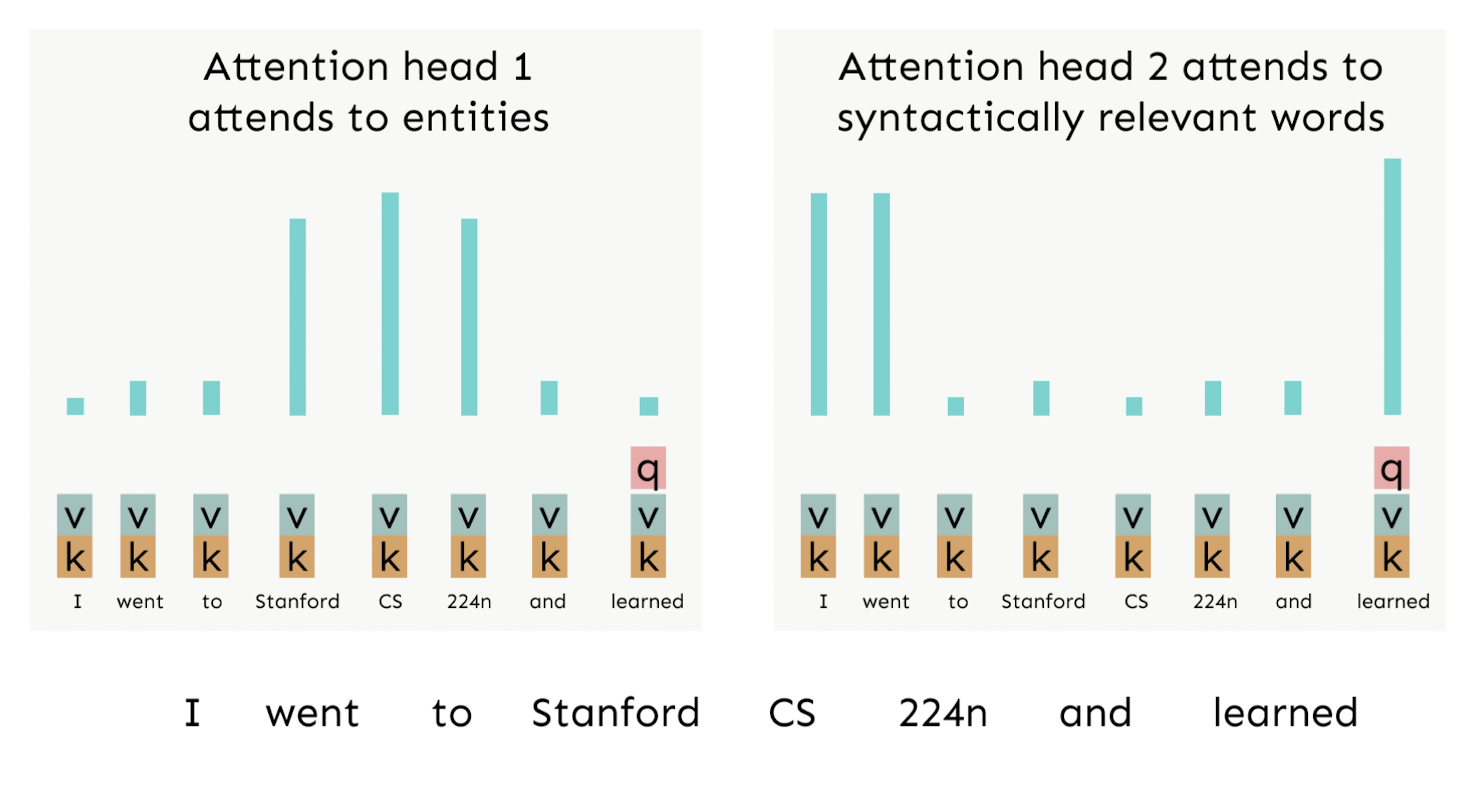
밑의 예시에서 'learned'에 대한 q, k, v가 있고, 파란색 bar를 통해 'learned'가 다른 단어들에 대해 얼마나 집중해야 하는지를 확인할 수 있다. 당연히 본인과는 q와 k의 유사도가 높을 것이므로 파란색 bar의 높이가 클 것이고 이외에도 'learned'는 'CS'에 집중해야 함을 알 수 있다.

self-attention의 과정을 더 자세히 살펴보면, 단어 w를 E행렬을 통해 임베딩 벡터 x로 바꾼다. 이때 단어 w는 원핫벡터로 표현되고 x의 shape는 dx1으로, d-dimension으로 나타낼 수 있다. 그리고 하나의 단어가 Q, K, V의 행렬과 곱해져서 각각 query, key, value으로 나타낼 수 있다. q와 k의 내적으로 각 단어의 attention score를 구하고, 이 값을 softmax를 거쳐(정규화 과정) 그 단어의 집중 정도를 구한다. 이 값을 이용해 value 벡터를 가중 평균해주면 해당 encoder hidden state의 attention output을 구할 수 있다.

그러나, self-attention에는 몇 가지의 barrier가 있다.
Barrier 1: does not have an inherent notion of order
self-attention은 순서 정보에 대해서는 알지 못하므로 문장 내 단어의 순서 인덱스를 벡터로 나타낸다. x의 크기는 dx1이고, 순서 인덱스 p의 크기도 dx1이다. 단어 임베딩 벡터 x와 순서 인덱스 벡터 p를 더함으로써 단어의 위치까지 고려한 워드 임베딩을 할 수 있다.
이러한 위치 벡터 p를 dxn의 행렬로 만들어 learnable parameter로 설정할 수 있다. 물론 단어들의 위치 인덱스를 학습할 수 있다는 장점이 있지만 만약 정해진 위치 인덱스를 벗어난 단어에 대해서는 외삽할 수 없다는 단점이 있다.
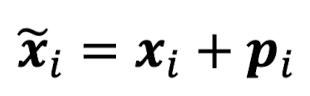
Barrier 2: no nonlinearities for deep learning! It's all just weighted average
만약 self-attention에 nonlinearities가 없고 그저 self-attention layer를 쌓기만 할 뿐이라면 벡터들의 평균을 계속해서 다시 구하는 것일 뿐이다. 이를 해결하기 위해 self-attention의 출력 벡터를 feed-forward network를 통해 후처리를 할 수 있다. 일반적으로 feed-forward network에는 한 층의 hidden layer와 activation function이 있어 nonlinearities를 더해줄 수 있다.
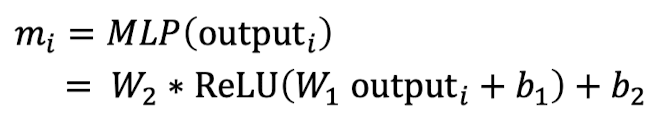

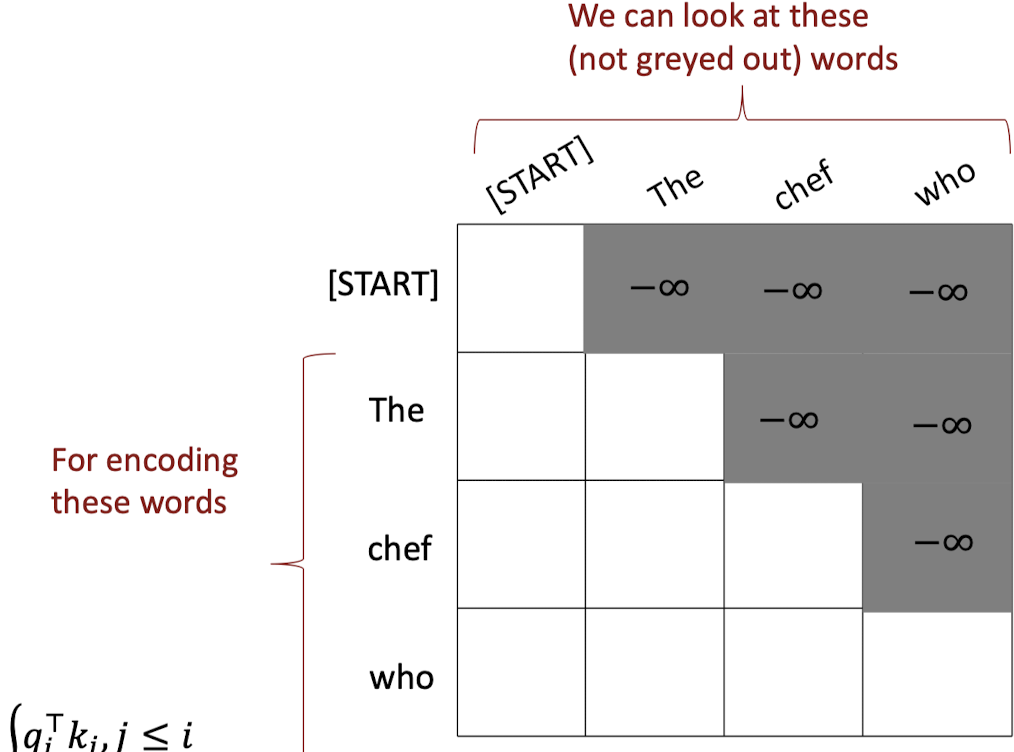
Barrier 3: need to ensure we don't look at the future when predicting a sequence
self-attention의 decoder가 sequence를 예측할 때 미래의 정답을 볼 수 없도록 해야 한다. 이를 해결하기 위해 미래의 단어들의 attention score를 -inf로 설정함으로써 미래 단어의 attention을 masking할 수 있다. 어떤 단어의 attention score가 -inf라면 이것에 exp를 취했을 때 0이 되기 때문에 가중치 \(\alpha\)는 0이 될 것이고, 결국 미래 단어는 attention output에 반영되지 않아 masking되는 효과가 있어 과거의 단어만 보고 다음 단어를 예측할 것이다.
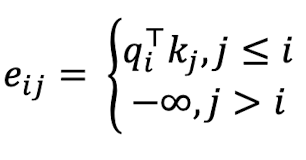
Summary
- position representation: 단어의 순서에 대한 정보가 담긴 벡터 p를 임베딩 벡터 x에 더해준다.
- masking: decoder에서 다음 단어를 예측할 때 미래의 시퀀스를 보지 못하게 해야 하므로 미래 단어들의 attention score를 -inf로 설정함으로써 masking하는 효과를 준다. 이는 masking을 병렬적으로 실행하면서도 과거의 정보만을 볼 수 있도록 한다.
- nonlinearites: self-attention의 output 벡터에 feed-forward network를 통해 후처리를 해준다(nonlinearities를 더해준다).
2. Transformer
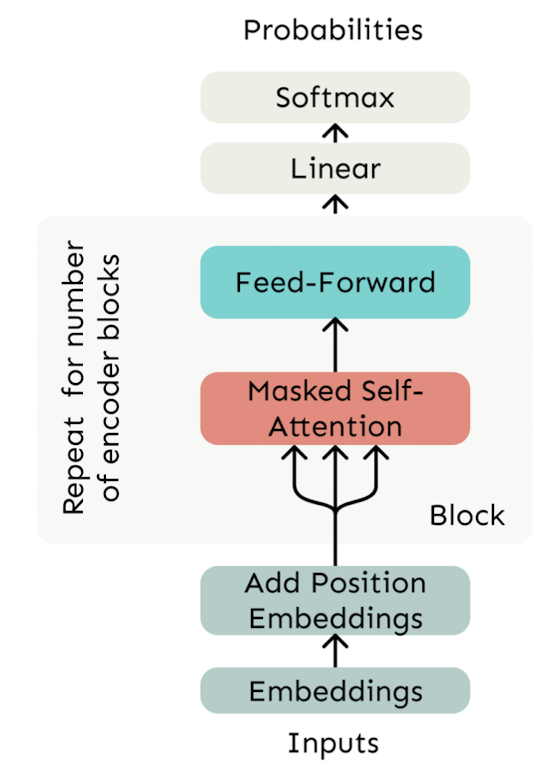
Transformer는 seq2seq모델에 attention과 self-attention의 개념을 추가한 것이다. Transformer의 전반적인 구조를 보면 다음과 같다.
- encoder
- 소스 시퀀스가 입력으로 주어지고 positional encoding을 거친다.
- encoder 블록 내에서 multi-head self-attention이 수행되어 소스 시퀀스 간의 관계가 학습된다.
- residual connection(add)과 layer normalization을 거친다.
- feed-forward network를 거쳐 비선형성을 더한다.
- encoder의 출력이 두 번째 decoder에 주어진다.
- decoder
- 타깃 시퀀스가 입력으로 주어지고 positional encoding을 거친다.
- 첫 번째 decoder 블록 내에서 masked multi-head self-attention이 수행되어 타깃 시퀀스 간의 관계가 학습된다. 이때 masking을 하여 미래 단어를 보지 못하게 한다.
- 두 번째 decoder 블록 내에서 multi-head cross-attention이 수행되어 소스 시퀀스와 타깃 시퀀스 간의 관계가 학습된다. 이때 cross-attention에서 encoder의 self-attention output이 각각 key와 value로 나타내어지고, decoder의 self-attention output이 query로 나타내어져 multi-head attention을 통과하게 된다.
- 만약 타깃 시퀀스의 첫 번째 단어가 입력으로 주어졌다면, output probabilities는 두 번째 단어가 무엇일지에 대한 확률 분포가 된다.
- 이때, transformer가 학습 중이라면 타깃 시퀀스의 각 토큰이 입력으로 주어지고 예측 중이라면 각 타임 스텝마다 모델이 예측한 단어가 다음 타임 스텝의 입력으로 주어지게 된다. 예를 들어 소스 시퀀스가 'I love cat'이고 타깃 시퀀스가 '나는 고양이를 사랑해'라면 학습 중인 decoder의 입력으로는 '나는', '고양이를', '사랑해'가 각각 주어지게 된다.
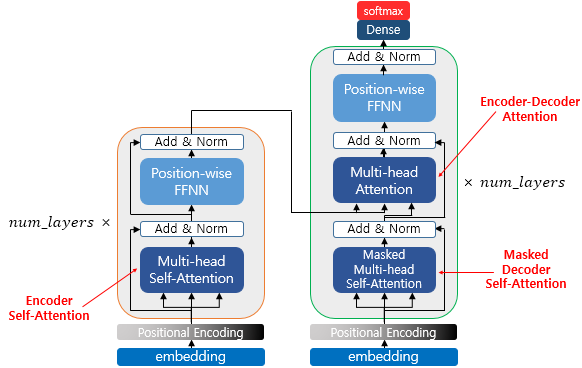


transformer 모델의 decoder 부분을 떼어서 보자면 다음과 같고, 이때 사용되는 여러 가지 개념에 대해 살펴보자.
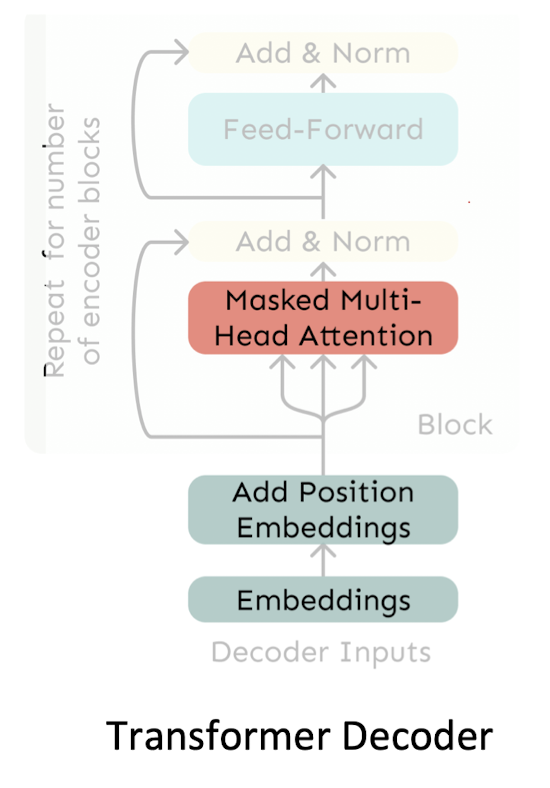
Multi-head self-attention
multi-head self-attention은 하나의 텍스트를 여러 개의 head가 읽는 것이다. 예를 들어 head1은 문장에서 중요한 의미를 갖는 단어에 집중하고 head2는 문장의 문법적 요소에 집중한다. 이처럼 하나의 문장에 attention을 적용할 때 다양한 결과가 나올 수 있기 때문에 여러 개의 head를 사용하는 것이다.
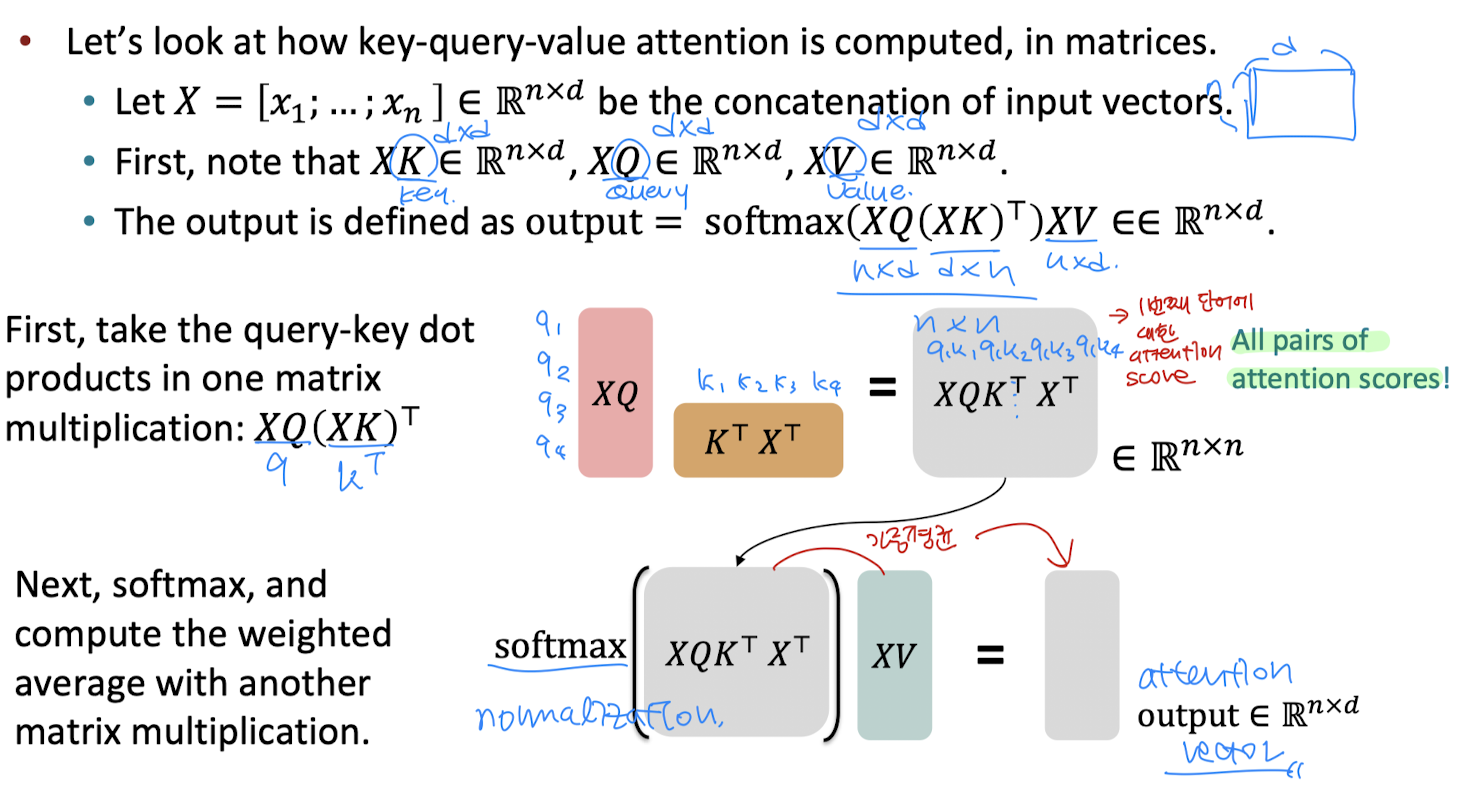
multi-head self-attention을 더 자세히 이해하기 위해 기존의 self-attention의 연산 과정을 살펴보자. 임베딩 벡터 X의 차원이 (n, d)라고 하고 이것에 (d, d)의 차원을 갖는 K, Q, V 행렬을 내적하여 입력을 key, query, value로 나타낼 수 있다. 이때 query와 key를 내적한 값이 attention score 행렬이 되고, 각각의 요소가 i와 j 단어 사이의 attention score가 된다. 이것에 softmax 함수를 취해준 뒤 value 벡터 행렬에 가중 평균을 해 주면 그것이 attention output이 되는 것이다.
그렇다면 multi-head self-attention의 연산은 어떨까? 기본적인 아이디어는 query와 key의 내적 결과가 가장 높은 단어 j에만 집중할 뿐 아니라 다른 j에도 집중하고 싶다는 것이다. 따라서 head마다 각각 다른 Q, K, V 행렬을 정의해야 한다. 원래 각 행렬의 차원은 (d, d)인데 h개의 head가 있다면 여러 개의 head로 쪼개진 각 행렬의 차원은 (d, d/h)가 된다.

여러 개의 head에 대해 self-attention을 수행하지만 효율적이다. 그 이유는 다음과 같다. 먼저, 임베딩 벡터를 Q행렬과 내적하면 그 차원은 (n, d)가 된다. 이때 이 차원을, (n, h, d/h)로 쪼개고 (h, n, d/h)로 transpose할 수 있다. 이때 h는 채널의 수이고 (n, d/h)는 각 head의 query의 차원이 된다. 이를 시각적으로 확인하면 아래와 같다. 결국 output은 3개의 head가 self-attention을 수행한 결과가 합쳐진 것이므로, 주어진 단어 간에 더 복잡하고 다양한 관계를 효율적으로 학습할 수 있다.

Scaled Dot Product
scaled dot product는 attention 연산을 할 때 스케일링에 도움을 주는 작업이다. 만약 차원 d가 매우 클 경우에 쿼리와 키 내적 행렬의 값들이 매우 커질 수 있다. 이것은 gradient가 작아지는 문제를 발생시키므로 내적값이 softmax function을 거치지 전에 scaling해줘야 한다. attention score를 d/h의 루트 값으로 나눠줌으로써 attention score가 매우 커지는 상황을 막을 수 있다.
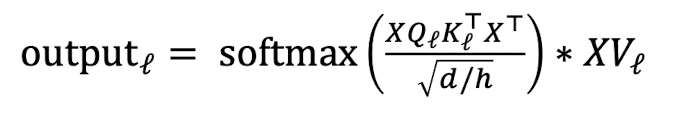
Residual Connection
layer에 x를 통과시킨 후, 그 결과에 x를 다시 더해준다. 이것이 좋은 이유는 gradient를 1로 만들어 소실 문제를 방지하기 때문이다. identity로 일종의 편향을 추가해준 것이라고 생각할 수 있다.

Layer Normalization
layer normalization의 아이디어는 hidden state의 값들에서 발생하는 uninformative variation을 평균과 표준편차를 이용해 정규화하자는 것이다. 아래 식을 사용하여 각 layer의 출력을 정규화해줄 수 있다.
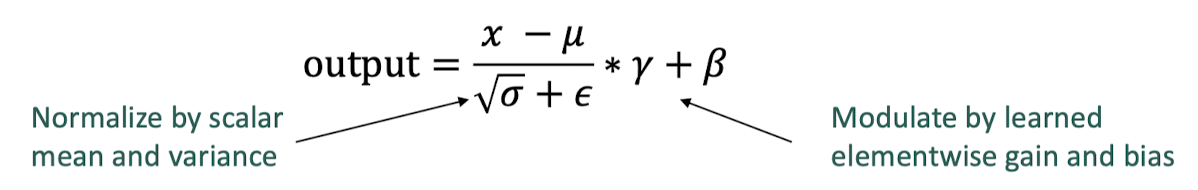
이제 다시 transformer의 encoder-decoder를 합친 것을 생각해보자. encoder는 bidirectional하게 소스 시퀀스를 인코딩한다. decoder는 unbidirectional하게 다음 단어를 예측한다.

What would like to fix about the Transformer?
그렇다면 transformer에서 고칠 것은 무엇이 있을까?
- Quadratic compute in self-attention
- 모든 단어 쌍에 대해 계산하는 것은 computation cost가 비싸다. 자기 자신까지 포함하고, 중복된 계산이 있고, d차원의 쿼리/키가 n개 있다고 했을 때 총 계산량은 \(O(n^{2}d\)이다.
- 따라서 self-attention의 계산 비용을 줄일 수 있는 방법을 생각해봐야 한다.
- 그러나 transformer 모델의 크기가 커질수록 self-attention의 quadratic 비용에도 불구하고 대부분의 계산 비용은 self-attention 외부에서 발생했다. 또한 일반적으로, 대부분의 self-attention 모델은 quadratic 이상의 비용을 쓰지 않는다.
- 놀랍게도, 대부분의 modification이 성능 향상에 큰 도움을 주지 못했다. -> 지금의 transformer가 최선으로 보인다.
- Position representation
- 위치를 나타내기 위한 심플한 방법이 있는가?
이 포스팅은 Standford CS 8단원에 기반하여 작성되었습니다.
'NLP > cs224n' 카테고리의 다른 글
| [cs224n] Prompting, RLHF (0) | 2024.07.05 |
|---|---|
| [cs224n] Pretraining (0) | 2024.07.03 |
| [cs224n] Translation, Seq2Seq, Attention (0) | 2024.07.02 |
| [cs224n] LSTM (Long Short-Term Memory) (1) | 2024.07.01 |
| [cs224n] RNN (0) | 2024.07.01 |