민공기

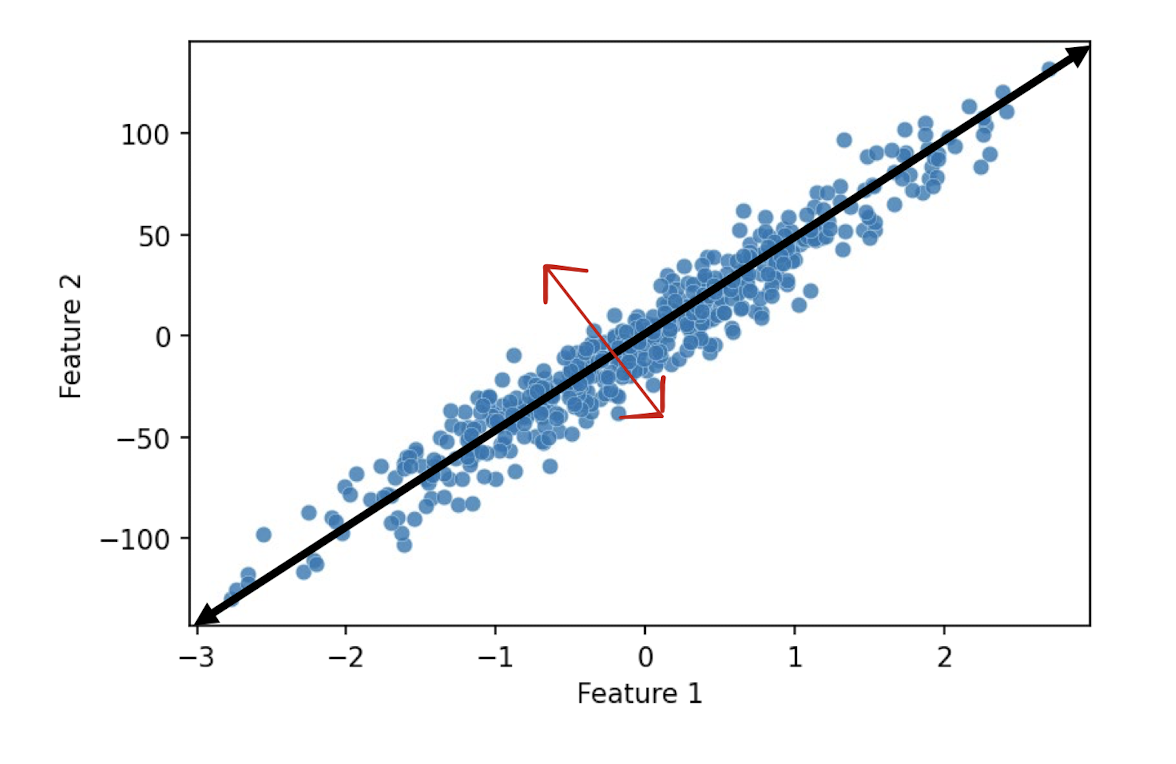
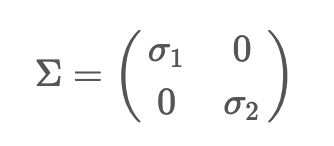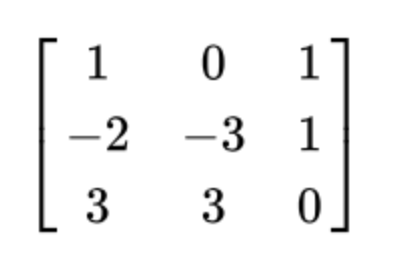SVD (Singular Value Decomposition)은 고유값 분해와 다르게 m != n인 (m, n)인 행렬에 대해서도 비대칭 행렬에 대해서도 모두 적용 가능한 행렬 분해법이다.  SVD는 임의의 (m, n) 행렬 A = \(U \sum V^T\)로 분해한다.A: (m, n) rectangular matrixU: (m, m) orthogonal matrix\(\sum\): (m, n) diagonal matrix\(V^T\): (n, n) orthogonal matrixorthogonal matrix란 \(U U^T = I\)가 되는 행렬, 즉 \(U^T = U^{-1}\)인 행렬이다. diagonal matrix는 주대각성분을 제외한 나머지 성분이 모두 0인 행렬이다.  SVD는 "직교하는 ..

선형 독립과 선형 종속같은 수의 성분을 가진 n개의 벡터 a_1, a_2...a_n에 대해 이들의 선형 결합인 c_1a_1 + c_2a_2 + ... c_nan_n = 0을 만족시키는 상수 c_1, c_2...c_n이 모두 0이면 벡터 a_1, a_2...a_n은 서로 선형 독립이다. 만약 c_1, c_2...c_n이 모두 0이 아니어도 위의 식을 만족한다면 그 벡터들은 서로 선형 종속이다.  기저 기저 (basis)란 어떤 벡터 공간에서 그 벡터 공간을 선형생성하는 선형독립인 벡터들의 집합이다. 즉, 어떤 벡터 공간의 임의의 벡터에게 선형결합을 통해 유일한 표현을 부여하는 벡터들의 집합이다.  예를 들어 2차원의 좌표평면이 있다고 하자. 그 좌표평면은 무수히 많은 벡터들로 이루어져 있는 하나의 벡터 공..

- 데이터의 불균형yes: 500, no: 268 심하지는 않지만 불균형 존재.  - 시각화단순히 yes/no 클래스에 대한 특징별 데이터 분포를 나타낸 것이 아니라, 의학적 지식을 이용해 특징별로 적절한 cutoff를 정한 뒤 cutoff 이하에서의 yes/no 클래스 비율, cutoff 이상에서의 yes/no 클래스 비율을 시각화함으로써 특징별로 어떻게 Outcome에 영향을 미치는 지 확인하고자 함. Pregnancies (3): 3번 이상 임신했을 경우 yes 클래스의 비율이 더 높게 나옴. 임신 중 인슐린이 정상적으로 분비되지 않음 + 인슐린 저항성이 생김 등의 문제로 인해 여러 차례 임신을 한 경우 당뇨병에 걸릴 확률이 높다고 해석할 수 있음. Glucose (126): 혈당이 높을수록 yes..

- nan을 모두 knn으로 채우기보다 시각화로 확인한 것들을 proportionally하게 채우기 + 나머지는 knn 사용이 더 높은 성능을 보임. (knn으로 채웠을 때 lightgbm 최고 성능: 0.4892 -> proportionally + knn으로 채웠을 때 lightgbm 최고 성능: 0.5067) - categorical variable을 str으로 바꾼 다음에 세분화하여 stepwise method로 feature selection하는 것보다 그냥 categorical을 하나의 변수로 보는 것이 더 좋은 성능이 나옴. (0.5019 -> 0.5068) - 총 세 가지 방법으로 데이터셋을 만듦1. nan까지 처리한 데이터에 standardization 적용한 데이터셋.- zero-cent..

어떤 머신 러닝 태스크의 최적 성능을 찾을 때, 어떤 하이퍼 파라미터를 이용하느냐는 어떤 모델을 사용하느냐 못지 않게 중요하다. 적절한 하이퍼 파라미터는 정해져 있지 않기 때문에 경험적으로 탐색하는 수밖에 없는데, gridsearch를 사용하는 것 역시 reasonable하지만 이산적으로 값을 탐색하기 때문에 그 한계가 있다. Bayesian optimization은 사용자가 하이퍼 파라미터의 범위를 정해주면 그 범위 안의 값들을 연속적으로 탐색하기 때문에 gridsearch보다 최적의 하이퍼 파라미터를 찾을 수 있게 된다.  Bayesian optimization은 관측 횟수, 즉 iteration 횟수가 많을수록 어떤 지점에서 최적값이 발생하는 지 (어떤 지점을 탐험해야 하는지) 확신하게 된다.  B..

What is PCA?    Principal Component Analysis (PCA)는 차원을 축소하는 unsupervised learning이다. 기법의 이름을 보면 유추할 수 있듯, PCA는 component feature만 남기고 다른 특징들을 제거해 차원을 축소한다.     만약 특징의 수가 매우 많을 때, 단순히 시각화만으로 데이터를 분석하기에는 한계가 있다. 따라서 어떤 특징이 가장 주요한 (component)지를 밝혀내어 dimension reduction, 즉 특징의 수를 줄이는 작업이 필요하다. PCA는 가장 큰 분산을 갖는 특징이 가장 주요한 특징이라는 사실을 이용한다. 큰 분산을 갖는 특징일수록 데이터를 더 많이 설명한다는 intuition이다. 즉, 높은 분산을 갖는 특징은 더..

Theory and IntuitionN-dimension을 가지는 공간이 있다고 해보자. Hyperplane은 그 공간을 두 부분으로 나누는 (N-1) dimension의 subspace이다. 예를 들어, 직선 (1-dimension)의 hyperplane은 점이고, 평면 (2-dimension)의 hyperplane은 직선이고, 3-dimension의 hyperplane은 평면이다. SVM의 주요 아이디어는, hyperplane을 사용해 분류 태스크를 수행할 수 있다는 것이다. 새로운 데이터가 들어왔을 때 hyperplane을 기준으로 어떤 클래스에 속하는 지를 판단할 수 있다.  더 구체적인 예시로 살펴보자. 직선의 hyperplane은 점이다. 아래와 같은 male/female 클래스를 점으로 분류..