01. 이전 내용
지지난 포스팅에서는 살사와 큐러닝을 배웠다. 살사는 아래와 같은 식을 이용해 큐함수를 업데이트하는 테이블 기반의 방법론이다. $$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t)$$ 살사는 한 번의 큐함수 업데이트에 (상태, 행동, 보상, 다음 상태, 다음 행동)이 필요하다. 그러나 \(\epsilon\)-탐욕 정책에 따라 행동하다 보면 다음 행동이 현재 행동의 큐함수에 영향을 미치기 때문에 잘못된 방향으로 학습할 수 있다. 이것이 바로 살사 (온 폴리시), 즉 행동 정책과 목표 정책이 같을 때의 한계였다. 그래서 살사의 보완점으로 등장한 방법론이 큐러닝, 다음 상태에 무조건 가장 큰 큐함수를 가지는 행동을 선택함으로써 행동 정책과 목표 정책을 분리하는 방법론이다. 행동 정책은 \(\epsilon\)-탐욕 정책을 이용하되 목표 정책은 탐욕 정책을 따른다.
지난 포스팅에서는 살사를 딥살사로 디벨롭시켰다. 딥살사는 살사의 식을 따르되, 인공신경망의 파라미터를 업데이트해 큐함수를 인공신경망으로 근사한다. 아래의 loss = (target - pred)^2를 최소화하도록 파라미터를 업데이트한다. 이때 인공신경망의 입력은 상태, 출력은 그 상태에서 할 수 있는 행동이다. $$ MSE Error = (R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t))^2$$
이번 포스팅에서는 큐러닝에 DNN을 적용한 DQN에 대해 다룬다. 큐러닝이란 (상태, 행동, 보상, 다음 상태)를 이용해 큐함수를 업데이트하는 방법이다. $$Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha (R_{t+1} + \gamma max_{a'} Q(S_{t+1}, a') - Q(S_t, A_t))$$ 큐러닝은 테이블 형식으로 큐함수를 저장하기 때문에 상태가 변하거나 무수히 많은 경우에는 사용이 제한된다. DQN (Deep Q-learning)은 큐러닝의 식을 따르되, 인공 신경망을 이용해 큐함수에 근사하여 테이블 형식의 한계를 극복했다.

02. DQN
카트폴 예제에 대해 알아보자. OpenAI는 Gym이라는 강화학습을 적용시킬 수 있는 여러 환경을 제공한다. 아래 그림처럼 검은색 사각형이 카드고, 갈색 막대가 폴이다. 에이전트가 해야 할 일은 폴이 쓰러지지 않도록 카트를 움직이는 것이다. 즉, 에이전트는 폴이 일정 각도 이상을 떨어지지 않게 하면서 화면에서 벗어나지 않게 하는 것을 학습해야 한다.

상태에 대한 정보는 4가지로, 카트의 수평선 상의 위치, 속도, 폴의 수직선으로부터 기운 각도와 각속도다. 이 경우, 이 게임에 존재하는 상태의 수는 어마어마하게 많을 것이기 때문에 이를 테이블 기반인 큐러닝으로 학습시킬 수 없다. 따라서, 큐함수를 인공신경망으로 근사시켜야 한다.

카트폴 예제는 간단하기 때문에 위에서 설명한 상태의 4가지 정보만으로 DQN 알고리즘을 수행할 수 있었다. 그러나, 좀 더 복잡한 문제에 대해 DQN은 CNN을 이용해 이미지를 넣어주면 그 이미지의 상태 정보를 추출해 각 행동의 큐함수를 근사할 수 있다. 즉, 인공신경망으로 CNN을 사용하고 입력은 이미지로 바꿔주면 된다. 아래는 DQN 알고리즘의 전체 파이프라인이다.
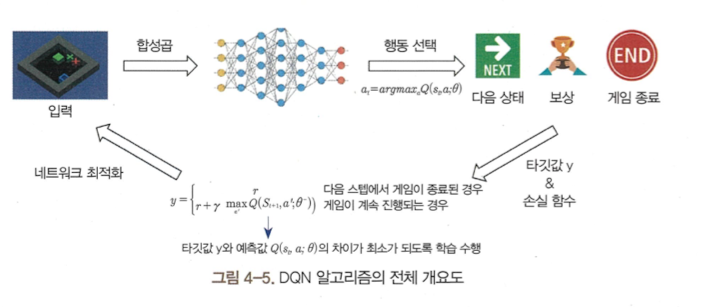
DQN은 오프 폴리시 알고리즘인 큐러닝과 인공 신경망을 결합한 가치 그래디언트 알고리즘으로, 결합을 위해선 경험 리플레이를 사용해야 한다. 또한 DQN은 타깃 신경망을 이용해 오프 폴리시를 구현한다. 경험 리플레이란 리플레이 메모리에서 에이전트가 환경을 탐험하며 얻은 샘플 (s, a, s', r)을 저장한다. DQN은 리플레이 메모리에서 batch_size만큼의 샘플을 랜덤으로 꺼내 학습하는 과정을 매 타임스텝마다 반복한다.
리플레이 메모리는 아래와 같은 특징을 가진다.
- queue 구조 (First in, First out 구조): 리플레이 메모리는 그 크기가 정해져 있기 때문에 메모리가 꽉 차면 맨 처음 들어온 샘플부터 데이터가 차례대로 삭제된다. 에피소드가 증가할수록 메모리에 양질의 샘플이 저장된다.
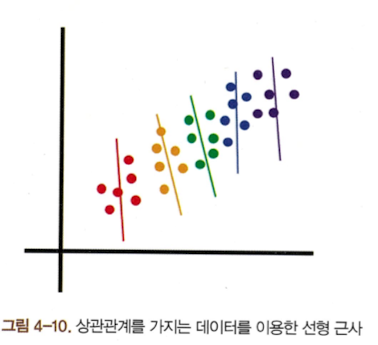
- 샘플 사이의 시간적 상관관계 제거: 딥살사의 경우 여전히 온폴리시 정책이기 때문에 현재 행동이 나쁘지 않아도 다음 행동이 나쁜 결과를 야기하면 현재 행동도 나쁘게 평가되었다. 즉, 샘플 사이에 시간적 상관관계가 있다. 따라서 시간적 상관관계가 있는 데이터로 인공신경망을 학습하면 그림 4-10처럼 전체 데이터의 특성을 학습하지 못한다. 그러나 리플레이 메모리는 메모리에서 샘플들을 랜덤으로 추출해 이를 학습에 사용하기 때문에 시간적 상관관계에 구애받지 않는다. 그림 4-11처럼 전반적인 데이터의 특성을 학습할 수 있게 된다.
- batched 샘플 이용: 딥살사는 매 타임 스텝마다 하나의 (s, a, s', r, a') 샘플을 이용해 큐함수 nn의 파라미터를 업데이트한다. DQN은 타임 스텝마다 업데이트를 하되, 리플레이 메모리에서 batch size만큼의 샘플을 랜덤 추출해 더 안정적으로 큐함수 nn의 파라미터를 업데이트한다.



DQN은 큐러닝의 연장선이기 때문에 마찬가지로 오프 폴리시다. 행동 정책과 목표 정책을 분리하기 때문에 DQN에서도 행동을 결정하는 신경망과 정답 (목표)를 결정하는 신경망을 분리해서 학습한다. 행동 결정 신경망은 매 타임 스텝마다 업데이트된다. 타깃 신경망은 매 타임 스텝마다 학습되지 않고 일정한 타임 스텝 이후에 행동 결정 신경망으로 대체된다.

DQN에서는 정답값으로 \(R_{t+1} + \gamma max Q(S_{t+1}, A_{t+1}, \theta^-)\)를, 예측값으로 \(Q(S_t, A_t, \theta)\)를 사용한다. 오차 함수는 MSE loss를 사용한다. \(\theta^-\)는 타깃 신경망의 파라미터, \(\theta\)는 행동 신경망의 파라미터다. 이때 파라미터 \(\theta\)는 매 타임 스텝마다 업데이트되고, 파라미터 \(\theta^-\)는 몇 타임 스텝 이후에 파라미터 \(\theta\)로 업데이트된다. 타깃 신경망을 매번 업데이트하지 않는 이유는 타깃 큐함수 역시 예측값으로, 불확실하기 때문이다. 이처럼 부트스트랩을 하는 과정에서 타깃 큐함수도 매 타임 스텝마다 업데이트되면 학습이 불안정해질 수 있기 때문에 타깃 신경망은 일정 시간 동안 업데이트하지 않고 유지한다.
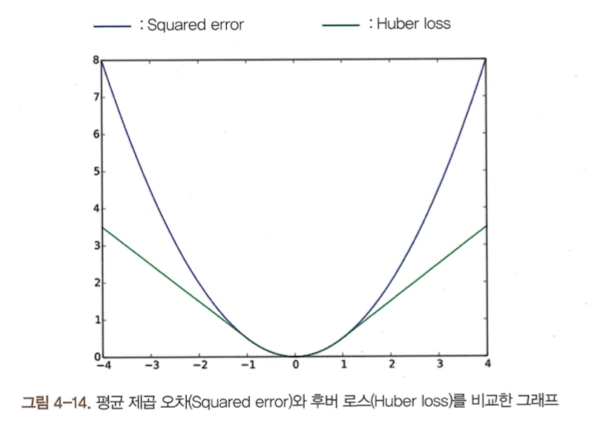
DQN의 인공신경망의 loss는 MSE와 Huber loss가 사용될 수 있다. $$MSE = (target - pred)^2 = (r + \gamma max_{a'} Q(s', a', \theta^-) - Q(s, a, \theta))^2$$

에이전트는 아래와 같은 과정을 거친다.
- 상태 s에 따른 행동 a 선택
- 환경으로부터 보상 r과 다음 상태 s'를 받음
- 샘플 (s, a, s', r)을 리플레이 메모리에 저장
- 리플레이 메모리에서 무작위로 추출한 샘플로 학습 (행동 인공신경망 업데이트): DQN의 행동 신경망의 입력은 딥살사와 마찬가지로 상태, 출력은 각 상태에서 행동 a를 했을 때의 큐함수다.
- 에피소드마다 타깃 신경망 업데이트
DQN의 한계는 다음과 같다.
- max-q-value를 과대 추정(overestimation)하는 경향이 있다. 부트스트랩을 사용하기 때문에 타깃 큐함수에 잡음이 발생하면 실제보다 큐함수가 더 커지는 현상이 발생한다. 이는 학습을 불안정하게 만든다.
- 어떤 상태가 좋은지 vs 어떤 행동이 좋은지를 구분하지 않는다.
- reward 값이 sparse한 환경에서는 학습이 느리다.
특히, DQN의 최대 행동 가치 함수를 과대 추정하는 한계를 완화하기 위해 두 개의 큐함수 근사 신경망을 정의하는 Double-DQN (DDQN)을 제시하게 된다. 먼저, \(argmax_{a} Q(s',a;\theta)\)에서 행동 결정 신경망의 파라미터 \(\theta\)를 갖는 인공신경망으로 큐함수를 근사하여 최대 큐함수를 갖는 행동을 선택한다. 이후 타깃 신경망의 파라미터 \(\theta^-\)를 이용해 그 결과를 평가한다.
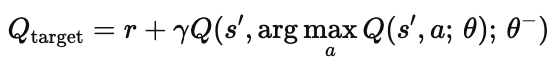

그러나 DDQN은 너무 보수적으로 학습할 가능성이 있고, reward 값이 sparse한 환경에서는 학습이 느리다는 것, 항상 DQN보다 성능이 우수하지 않다는 등의 한계가 있다.
Dueling-DQN은 큐함수를 상태 가치 함수와 이득 함수로 분해한다. 이때 상태 가치 함수 V(s)는 상태 s에 있는 것이 얼마나 좋은 것인지를, 이득 함수 A(s, a)는 상태 s에서 행동 a를 하는 것이 얼마나 좋은지를 나타낸다. (큐함수는 상태 s에서 행동 a를 한 후 정책을 따랐을 때 얻을 수 있는 총보상의 기댓값, 이득 함수는 큐함수에서 가치 함수를 뺀 값으로, 상태 s에서 다른 행동에 대한 상대적인 가치를 의미한다.)

근데 위 식으로 큐함수를 계산하면 V(s)와 A(s, a)가 각각 어떤 값인지 모르기 때문에 (V와 A가 유일하지 않음; unidentifiable 문제) 아래의 식으로 큐함수를 근사한다. (잘 이해하진 못했다,,)


Dueling-DQN은 적은 수의 행동이 있는 환경에선 효과가 거의 없고, 구조 복잡도가 증가하고, V와 A를 따로 학습하기 때문에 불안정하게 학습될 수 있다.
'RL' 카테고리의 다른 글
| LLM과 강화학습 (0) | 2025.03.10 |
|---|---|
| 강화학습: 정리 (0) | 2025.02.21 |
| 강화학습: 가치 그래디언트 (딥살사)와 정책 그레디언트 (REINFORCE 알고리즘) (0) | 2025.02.20 |
| 강화학습: SARSA와 Q-Learning (0) | 2025.02.18 |
| 강화학습: 다이나믹 프로그래밍으로 최적 정책 구하기 (0) | 2025.02.18 |