01. 다이나믹 프로그래밍
다이나믹 프로그래밍이란 하나의 큰 문제를 여러 개의 작은 문제로 쪼갠 후, 단계적으로 작은 문제를 해결하고 저장하며 결과적으로 큰 문제를 해결하는 방법론이다. 그러나, 강화학습을 다이나믹 프로그래밍으로 해결하려면 보상 함수와 상태 전이 함수 (상태 s에서 행동 a를 했을 때 상태 s'로 전이될 확률)를 모두 알아야 하고, 이 두 가지 요소를 모든 상태와 행동에 대해 알기는 불가능에 가깝다 (DP는 model-based). '보상 함수를 안다'라는 것은 말 그대로 에이전트가 보상을 다 안다는 말이고, 지도로 길 찾기로 예를 들면 목적지까지 가는 데 속도, 방향, 지름길 등을 다 알고 있는 경우다. 반면 현재의 강화학습은 model-free로, 다이나믹 프로그래밍과 다르게 에이전트가 모든 환경을 다 안다는 전제로 가치 함수를 계산하지 않고 환경으로부터 얻은 샘플을 통해 탐색하는 방식이기 때문에 환경의 보상 함수와 상태 전이 확률을 완벽히 알 필요 없다. 즉, 강화학습은 환경에 정의된 보상을 에이전트가 모르고 경험을 통해 탐색하는 방식이다. 지도로 길 찾기로 예를 들면 그냥 지도만 띡 주어주고 에이전트로 하여금 여러 경로로 가 보면서 보상을 탐색해서 최적의 길을 찾으라는 태스크를 해결하는 것이다. 그럼에도 우리가 다이나믹 프로그래밍을 알아야 하는 이유는, 강화학습이 다이나믹 프로그래밍을 기반으로 발전했기 때문이다. 다이나믹 프로그래밍을 이용해 문제를 푸는 방법론 (강화학습에서는 최적 정책을 구하는 방법론)은 정책 이터레이션과 가치 이터레이션이 있다.
02. 정책 이터레이션
정책 이터레이션은 현재의 정책을 따랐을 때의 가치 함수를 계산하고 (정책 평가), 구한 가치 함수를 토대로 정책을 업데이트 (정책 발전)하는 과정을 반복하여 최적 정책을 구한다. 정책 평가 과정에서 가치 함수를 구할 때 벨만 기대 방정식을 이용하고 정책 발전 과정에서 정책을 탐욕적으로 발전시킨다.

- 정책 평가: 현재 정책을 따랐을 때의 가치 함수 (총보상의 기댓값)를 벨만 기대 방정식을 이용해 구한다. 벨만 기대 방정식은 현재 상태에서의 가치 함수와 다음 상태에서의 가치 함수의 관계식이다. 벨만 기대 방정식은 \(v_{\pi}(s)\) = \(v_{\pi}(s')\)를 만족시키는 가치 함수 \(v_{\pi}(s)\)를 찾는다. 정책 평가를 하기 위해 에이전트는 모든 상태 s를 돌아다니며 상태 s에 대한 가치 함수를 구하고 저장된 값을 갱신한다.

- 정책 발전: 현재 정책을 따랐을 때 모든 상태에 대한 가치 함수를 계산했다면, 이제 이를 토대로 현재 정책을 발전시켜야 한다. 모든 상태에 대한 가치 함수를 계산했으므로 어떤 상태 s에서 어떤 행동 a를 했을 때의 보상인 큐함수를 구할 수 있다. 어떤 상태 s에서 여러 개의 행동을 할 수 있을 텐데, 그 중에서 최대의 큐함수를 갖는 행동이 높은 확률을 갖도록 탐욕적으로 정책을 조정한다. 만약 최대의 큐함수를 내는 행동이 a로 1개라면 \(\pi(a|s)\) = 1, 여러 개라면 1을 동일하게 나눠서 배정한다.

예시를 들어 어떻게 정책 이터레이션이 최적 정책으로 수렴하는지 알아보자.
- 셋팅: 벨만 기대 방정식, 큐함수 계산식, 할인율, 초기 정책
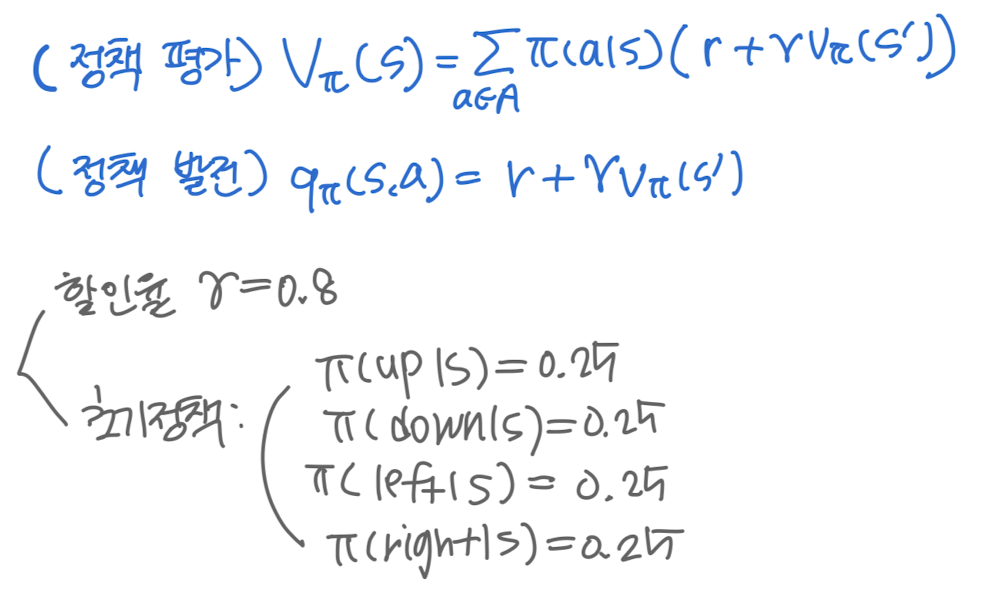
- 정책 평가: 현재 정책을 이용해 각 상태에 대한 가치 함수 구하기 -> $$v_{\pi}(s) = \sum_{a \in A} \pi(a|s) [r(s, a) + \gamma v_{\pi}(s')]$$ 이용

- 정책 발전: 구한 가치 함수, 정확히는 큐함수를 토대로 정책을 업데이트. 이때, 큐함수를 계산할 때 사용되는 \(v_{\pi}(s')\)는 업데이트 전 값을 사용한다. -> $$\pi(a|s) = argmax_{a} [r(s, a) + \gamma v_{\pi}(s')]$$ 이용


첫 번째 이터레이션 (정책 평가, 정책 발전)을 수행한 결과는 위와 같다. 정책 발전의 결과로 정책이 갱신되었으니, 이를 기반으로 또 각 상태에 대한 가치 함수를 계산하는 정책 평가를 한다. 정책이 바뀌었으니 각 상태의 가치 함수도 첫 번째와 다르게 계산될 것이다. 가치 함수도 노란색 하이라이트로 바뀌었으니 큐함수도 다르게 계산된다. 각 상태에서 최대의 큐함수를 갖는 행동에게 높은 확률을 부여하여 정책을 업데이트한다. 이 과정을 계속 반복하면 결국 아래와 같은 화살표 방향으로 움직이도록 정책이 형성된다. -1은 피하면서 목적지로 향하도록 에이전트는 행동한다. 반복 종료 조건은 가치 함수가 더 이상 업데이트되지 않을 때까지다. (벨만 기대 방정식의 참 가치 함수를 구할 때까지)

정책 이터레이션은 아래와 같은 한계를 갖는다.
- 정책 발전은 정책 평가 종료 후에만 가능하다.
- 한 번의 정책 평가에서 모든 상태에 대한 가치 함수를 계산해야 하므로 계산량이 많다.
- 그 많은 연산 중에서 의미 없는 연산을 반복해야 할 수 있다.
03. 가치 이터레이션
가치 이터레이션은 정책 이터레이션과 다르게 벨만 최적 방정식을 이용한다. 벨만 기대 방정식과 벨만 최적 방정식의 차이점은, 벨만 기대 방정식은 어떤 상태 s에서 행동 a를 취할 확률을 모든 행동에 대해 부여하는 형태지만 벨만 최적 방정식은 하나의 최적의 행동 a에만 확률을 부여하는 결정론적인 형태다. 물론 초기의 정책은 임의로 정한 엉터리이기 때문에 처음 정책을 따랐을 때가 최적이 아닐 수 있다. 그러나 정책 이터레이션이든 가치 이터레이션이든 다이나믹 프로그래밍을 하려면 어쨌든 반복적인 수행이 필요하다. 따라서 초기에 엉터리고 결정론적으로 행동함에도 결국 반복을 통해 어떤 상태에서 하나의 최적의 행동을 할 수 있다는 것이다.
정책 이터레이션의 가치 함수 식을 보면 정책 \(\pi(a|s)\)를 고려한다. 그러나 가치 이터레이션에서는 어떤 상태 s에서 어떤 행동 a를 했을 대의 보상인 큐함수의 최대값을 그 상태에서의 가치 함수로 판단한다. $$v_{\pi}(s) = max_{a \in A} q_{\pi}(s, a) = max_{a \in A} (r(s, a) + \gamma v_{\pi}(s'))$$
즉, 최대의 큐함수를 갖는 행동 a를 하는 확률만을 1로 설정하고 나머지는 0으로 설정하는 것과 같다.

따라서 정책을 별도로 업데이트하는 과정 없이 바로 다음 가치 함수를 계산한다. 이 과정을 계속 반복한다. 종료 조건이 된다면 이제 각 상태에마다 최종 가치 함수가 매겨질 것이다. 이 가치 함수를 이용해 정책을 완성할 수 있다. $$q_{\pi}(s, a) = max_{a \in A} (r(s, a) + \gamma v_{\pi}(s'))$$ 위 식을 이용해 어떤 상태 s에서 어떤 행동 a를 했을 때의 보상인 큐함수를 구하고, 그 중에서 최대의 큐함수를 가지는 행동을 하도록 정책을 설정한다. 즉, 가치 이터레이션은 벨만 최적 방정식을 이용해 정책 이터레이션처럼 정책을 명시적으로 업데이트하지 않고도 최종적으로 봤을 때에는 최적의 정책에 수렴할 수 있도록 한다.
정책 이터레이션과 셋팅이 같다고 하고 가치 이터레이션의 예제를 보자. 가치 이터레이션은 정책 이터레이션과 달리 정책 평가에서 벨만 최적 방정식을 이용하고 매 이터레이션마다 명시적인 정책 발전 과정이 없다. 매 이터레이션마다 벨만 최적 방정식을 이용해 각 상태에서의 가치 함수를 업데이트한 뒤, 이터레이션이 모두 끝나면 각 상태에서 큐함수를 최대화하는 행동에게 높은 정책을 주는 방식으로 마무리한다.
가치 함수 계산 식: \(v_{\pi}(s) = max_{a}[r(s, a) + \gamma v_{\pi}(s')]\)
최종 정책 계산 식: \(\pi(a|s) = argmax_{a}[r(s, a) + \gamma v_{\pi}(s')]\)


04. GPI
GPI (Generalized Policy Iteration)은 정책 평가와 정책 발전이 상호작용하는 구조를 의미한다. 가치 함수는 현재 정책을 따른 때 안정화될 수 있고 현재 정책은 계산된 가치 함수를 탐욕적으로 고려함으로써 안정화된다. 즉, GPI에서 평가와 발전은 경쟁적인 동시에 협력적이다. 서로를 평가하고 발전시키지만 최적 가치 함수라는 공통해를 찾는다.
05. 퀴즈
- 다이나믹 프로그래밍의 의의? - 다이나믹 프로그래밍이란 큰 하나의 문제를 여러 개의 작은 문제로 나눈 뒤, 작은 문제를 순차적으로 해결하여 결국 큰 문제를 해결하는 방법론이다. 강화학습의 경우, 다이나믹 프로그래밍을 사용하면 보상 함수와 상태 전이 함수를 모두 알아야 하기 때문에 현재의 강화학습에서는 사용하지 않는 방법론이지만 다이나믹 프로그래밍은 강화학습의 기반이라는 점에서 의의가 있다.
- 정책 평가 종료 이후에만 정책 발전이 이루어지는 것의 단점은? - 정책 이터레이션은 현재의 정책을 따랐을 때의 가치 함수를 구하는 정책 평가와 구한 가치 함수를 바탕으로 정책을 갱신하는 정책 발전으로 이루어져 있다. 정책 이터레이션은 반복할수록 불필요한 연산량이 늘어나는데, 꼭 정책 평가 종료 이후에만 정책 발전이 이루어지는 것은 비효율적이다.
- 정책 이터레이션에서는 초기 정책이 존재하지 않는다(o/x) - x. 정책 이터레이션에서는 가치 함수를 계산할 때 정책이 사용되기 때문에 초기 정책이 필요하다. 반면 가치 이터레이션에서는 최대 큐함수로 가치 함수가 갱신되기 때문에 초기 정책이 필요 없고 (벨만 최적 방정식의 계산에 정책이 필요 없고), 다만 각 상태의 보상과 초기 가치 함수는 필요하다.
- 정책 이터레이션에서 정책 발전이 큐함수 값과 상태 가치 함수 값을 비교하는 이유는 무엇인가? - 어떤 상태 s에서 어떤 행동 a를 하는 것이 이득이 되는가를 알고, 이득이 되면 그 행동을 하도록 확률을 높게 설정하고 이득이 되지 않으면 그 행동에 대한 확률을 낮게 설정하기 위해서이다. 예를 들어 위 본문의 예시에서 정책 평가 과정에서 벨만 기대 방정식을 이용해 각 상태의 가치 함수를 계산했다. 이때 가치 함수는 정책 x 상태 s에서 행동 a를 했을 때의 가치 함수 (큐함수)를 모두 더한 것이다. 이때 큐함수는 계산된 가치 함수보다 크거나 같거나 작거나 할 것이다. 만약 큐함수가 가치 함수보다 크거나 같다면 상태 s에서 행동 a를 한 것의 가치가 높은 것이기 때문에 높은 정책을 부여해야 한다. 반대로 큐함수가 가치 함수보다 작다면 상태 s에서 그 행동 a를 한 것의 가치가 낮은 것이기 때문에 낮은 정책을 부여해야 한다. 즉, 정책 이터레이션의 정책 발전이 큐함수 값과 상태 가치 함수 값을 비교하는 이유는 정책을 올바르게 설정하기 위해서이다.
- end-point에서의 정책은 무엇인가? - end-point에서는 그냥 제자리에 있어야 하기 때문에 모든 행동에 대한 확률이 0이다.
'RL' 카테고리의 다른 글
| 강화학습: 정리 (0) | 2025.02.21 |
|---|---|
| 강화학습: DQN (0) | 2025.02.21 |
| 강화학습: 가치 그래디언트 (딥살사)와 정책 그레디언트 (REINFORCE 알고리즘) (0) | 2025.02.20 |
| 강화학습: SARSA와 Q-Learning (0) | 2025.02.18 |
| 강화학습: 강화학습이란? (0) | 2025.02.17 |